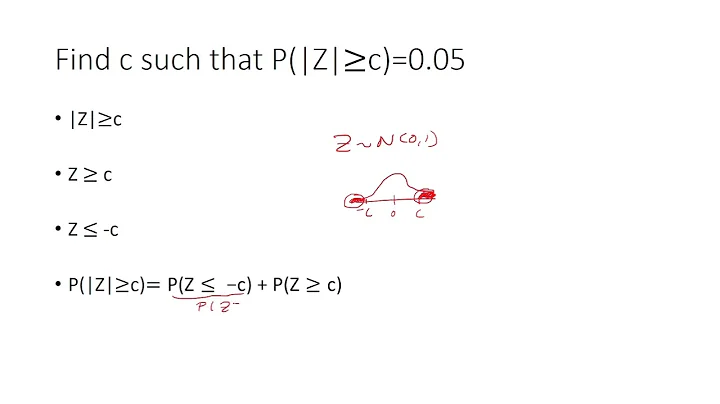
12.05.2024

We want to find C such that the. probability of the absolute value of Z. is greater than or equal to C. that is equal to 0.05. . so let's focus on the absolute value. of Z being greater than or equal to C. there's going to be two cases the first. case when we remove the absolute value. in the second case we flip the. inequality. and then put a negative in front of C. so looking at the probability that the. absolute value of Z is greater than or. equal to C. we break it up into probability Z is. less than or equal to negative C plus. the probability of Z is greater than. equal to C. now we're looking Z at Z here being a. normal distribution with mean zero and. standard deviation one so this is going. to be symmetric. at zero. so if we're looking at the probability Z. is greater than or equal to C that's. going to be this area.

And prolocation probability Z is less. than equal to negative C that's going to. be this area. and because this is symmetric finding. this area is the same thing as finding. this area. so this area right here is just the same. thing as probability Z is greater than. or equal to C. so there's going to be two of those. so that is going to equal the 0.05. because remember this is equal to 0.05. from the given dividing both sides by 2. we get the probability that Z is greater. than or equal to C is 0.025. now. again here what we're saying is. that this area right here. is 0.025 which is the same thing as. saying that this area right here. is 0.975. so if we do the complement of 1 minus. probability of Z less than equal to C is. 0.025 we see that the probability of Z. is less than or equal to C is 0.975. now we want to solve for C so we do the.

inverse Norm. of 0.975 and we get that is equal to. 1.96 which is C